２本の（省略付き）棒グラフを思いのまま描く方法

例えば、こんなふたつの値があったとしましょう。

Country name	GDP (US$)
China	7,318,499,269,769
Japan	5,867,154,491,918

そのままグラフを作ると 差が少なくて見栄えが悪い の。

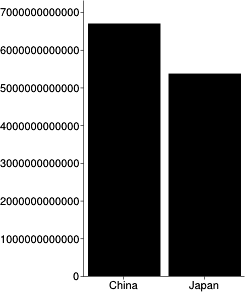
そんなときの簡単な省略棒グラフの描き方

まずは、枠の中に高さの違う棒（四角形）を２つ描きます。 棒の高さは 差をぐいっと付けて 描きます。 どの程度、差を付けるかは お好みで調整してね 。

大きい方に合わせて線を引いて大きい方の数字を、 小さい方に合わせて線を引いて小さい方の数字を書き入れます。 値が大きいので billion で区切って、7318 と 5867 を書き入れました。 また、棒の下にはラベルも書きましょう。 もちろん、高い棒の方が China ですね。

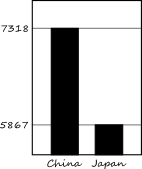
最後に左下に省略線と数字のゼロを入れるだけ。

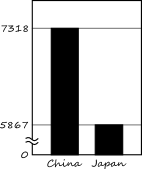
見栄えが気に入らないのなら、お好みで色なり線を工夫してみてね☆彡

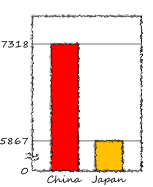
このやり方で省略棒グラフとして正しいことの数学的議論

2つのデータがあって、それぞれの値が V₁, V₂ とする。 それぞれに対応する棒グラフの高さが h₁, h₂ とし（単位はセンチメートルなどの長さ）、 省略グラフの波線によって E だけ省略されているとする。

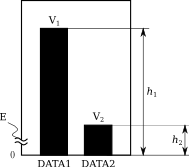
このとき、

が成り立つ任意の V₁, V₂, h₁, h₂ (V₁ > V₂ > 0, h₁ > h₂ > 0) に対してE(> 0)が存在することを以下に示す。

もし省略部のない単なる棒グラフの場合、 V₁, h₁と V₂, h₂ の比は同じになるように、棒グラフを描く必要がある。 よって、省略部のない単なる棒グラフの場合下式が成り立つ。

省略部のある棒グラフでは h₁, h₂ がそれぞれEだけ省略されているので、 上の式を h₁ → (h₁ + E), h₂ → (h₂ + E) を書き換えた、下式が成り立たなければならない。

これを解くと E は下記の値となる。

ここで

から

が求まるので、今求めたEの値は正の数である。

QED.

上の証明の考察

上の証明で最初に与えた条件式

は、実際の値の比(V₁ ÷ V₂) よりもグラフの上の棒の高さの比 (h₁ ÷ h₂) が大きいということを表す。

この前提下では、任意のデータ、任意の棒の高さで省略付き棒グラフが描ける。 というのも、任意のデータ、任意の棒の高さに対して、省略線で省略された棒の高さ(E)が求められるからである。

結論1: このやり方は実際の値の比よりもグラフの上の棒の高さの比が大きいという前提下で任意のデータ、任意の棒の高さで省略付き棒グラフが描ける

逆に

すなわち、実際の値の比(V₁ ÷ V₂) よりもグラフの上の棒の高さの比 (h₁ ÷ h₂) が小さい場合、省略線で省略された棒の高さ(E)が負になってしまう。 これは具体的には下記のようなことであり、省略によって棒の高さを減じなければならないのに、 棒の高さが水増し、という意味不明なことになっている。 これは明らかにおかしい。

Country name	GDP (US$)
China	7,318,499,269,769
Palau	165,517,314

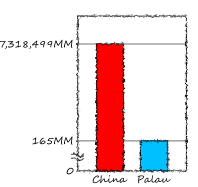
結論2: 省略棒グラフは、元のデータの変化の比を強調して表示できる。しかし、元のデータの変化の比を縮めて表示することはできない。

まとめ

以上の考察によって、2本の 省略棒グラフは、以下の特徴を持つことがわかった。

• 実際の値の比よりもグラフの上の棒の高さの比が大きいという前提下で任意のデータに対して、任意の棒の高さで描くことができる。すなわち、棒の高さや高さの差にまったく意味はない。
• 2つの値の 差比がたいしたことがない ことがわかる。

補足

• 本稿では、3本以上の省略棒グラフについては言及はしていないし、善悪も言及していない。
  • 3本以上の省略棒グラフでは、差の束縛条件が加わるため、「棒の高さの差にまったく意味がない」ということはなくなる。
  • 「棒の高さの差」には意味が生じるので、批評の観点としては、人間が見た「印象」を考慮に入れた議論となる。
  • よって、3本以上の省略棒グラフの善悪の議論には、純粋な数式では答えは導き出せないのである。
• 本稿は GDP を単なる手頃なデータとして使っただけであり、例えば中国の GDP について強調しようとしたわけではない。

参考文献

• GDP (current US$), The World Bank, 2011.
• Re: 悪いグラフの例|3D円グラフにご注意, commented by x-rebuttal, スラッシュ・ドット・ジャパン, 2008.