二次方程式
a
x
2
+
b
x
+
c
=
0
ax^2 + bx + c = 0
(1.1)
の解は、下記の公式であたえられる
x
=
−
b
±
b
2
−
4
a
c
2
a
x = {-b \pm \sqrt{b^2-4ac} \over 2a}
(1.2)
ここで、判別式(discriminant)とよばれるルートの中身
b 2 − 4 a c b^2-4ac
の値が負になるとき、実数解を持たない。これを複素数を導入することで判別式が負になるときも解(虚数解)が与えられる。
ここで登場する二乗すると-1になる虚数単位i はしばしば高校の数学教師は存在しないと言ったりするがそれはナンセンスな話である。
アイは院のサロンで、数人の院生と共に教授と話していた。何の流れだったか、 存在、非存在の話になった。アイが教授に高校時代、数学教師(アテネだ!)から「この世界にアイは存在しません」と聞いた、という話をしたとき、彼は、
―― 西加南子『i』ポプラ社、2016年
実際には実数を表した数直線(実軸; real axis)と90度をなす新たな数直線(虚軸; imaginary axis)を導入した虚数平面(complex plane)として目に見える=存在する形で扱うことができる。(だから、実軸上には 存在しないといった言い方ならば理にかなっている。)
そこで本稿では、しばしば存在しないと言われてしまう虚数解について、実際に存在を目で見ることによって確認したい。
二次方程式の虚数解の図示やネット上に数多あって、例えば下記のようなページがある。
ただいずれも図を描くためのコードは公開されておらず読者がプログラミングをする必要がある。
本稿ではすべての図について、 gnuplot のコードを付けた。
また、グラフの概形について考察も掘り下げる。
複素解析でよくある可視化
domain coloring の導入
複素関数を素直にグラフで図示しようとすると、関数の引数の実軸・虚軸、関数値の実軸・虚軸の合計4軸必要となり、現実的に表現できない。
そこで複素解析学(complex analysis)では、関数値の偏角を色相(hue)にマッピングして表すことで、この図示の困難を克服することがしばしば行われる(domain coloringと呼ばれる)。
例えば
f
(
x
)
=
x
f(x)=x
をこの方式で表すと下記のようになる。
Fig-1.1 f(x)=x
上図を出力するための gnuplot のコード
#!/usr/bin/gnuplot
set cbrange [-pi:pi]
set cbtics ("-π" -pi, "0" 0, "π" pi)
set pm3d corners2color c1
set palette defined ( 0 0 1 1, 1 1 1 1 )
set isosamples 100, 100
set palette model HSV defined ( 0 0.5 1 1, 0.5 1 1 1, 0.5 0 1 1, 1 0.5 1 1 )
#set palette model HSV start 0.5 defined (0 0 1 1, 1 1 1 1)
set xlabel "real"
set ylabel "imag"
set nokey
set isosamples 512, 512
set size square
I = {0,1}
f(x) = x
splot '++' using 1:2:(abs(f(x+I*y))):(arg(f(x+I*y))) with pm3d
グラフ上の上方向の高さは絶対値を使っているので、まんなかの 0 がグラフの視覚的に最も低い場所になる。
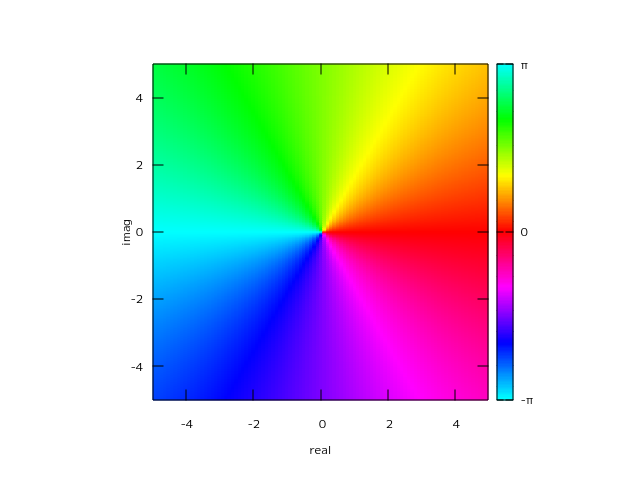
偏角を確認するために、この三次元グラフの真上から覗くと下図のようになる。
Fig-1.2 argument of f(x)=x
上図を出力するための gnuplot のコード
#!/usr/bin/gnuplot
set cbrange [-pi:pi]
set cbtics ("-π" -pi, "0" 0, "π" pi)
set pm3d corners2color c1
set palette defined ( 0 0 1 1, 1 1 1 1 )
set isosamples 100, 100
set palette model HSV defined ( 0 0.5 1 1, 0.5 1 1 1, 0.5 0 1 1, 1 0.5 1 1 )
#set palette model HSV start 0.5 defined (0 0 1 1, 1 1 1 1)
set xlabel "real"
set ylabel "imag"
set nokey
set isosamples 512, 512
set size square
set xrange [-5:5]
set yrange [-5:5]
set view map
I = {0,1}
f(x) = x
splot '++' using 1:2:(abs(f(x+I*y))):(arg(f(x+I*y))) with pm3d
pause -1
1 は偏角 0 度なので赤、虚数単位 i は偏角 90 度なので緑、-1 は 180 度で水色、-i は 270 度で青紫色、のように表示される。
複素解析では複素関数の関数値が0となる点をゼロ点 (zero) と呼ばれるが、domain coloring ではゼロ点の近傍は半時計回りに色相が変化するような絵面になる。
二次関数の domain coloring 表示
二次関数を解析するにあたり、簡単のため下記の関数で考えるものとする。
f
(
x
)
=
x
2
+
h
f(x)=x^2+h
(1.3)
この(1.3)に対して
x
→
x
−
−
b
2
a
,
y
→
a
−
1
(
y
−
(
c
−
a
(
−
b
2
a
)
2
−
h
a
)
)
x \to x - \frac{-b}{2a}, y \to a^{-1} \left(y-\left(c-a\left(\frac{-b}{2a}\right)^2-ha\right)\right)
という操作を行うと、(1.1)の左辺と同じになる。
すなわち(1.3)から x 軸方向への平行移動、y軸方向への平行移動および拡大縮小操作を組み合わせることで(1.1)の左辺が求められる。
だから(1.3)を考えて、後はこれを水平移動および拡大縮小操作を施されたものとして考えれば良い。
(1.3)がゼロとなる方程式の解は h < 0 のとき実数解を2個持ち、 h = 0 のとき x = 0 で重解となり、 h > 0 のとき虚数解を 2 個持つ。
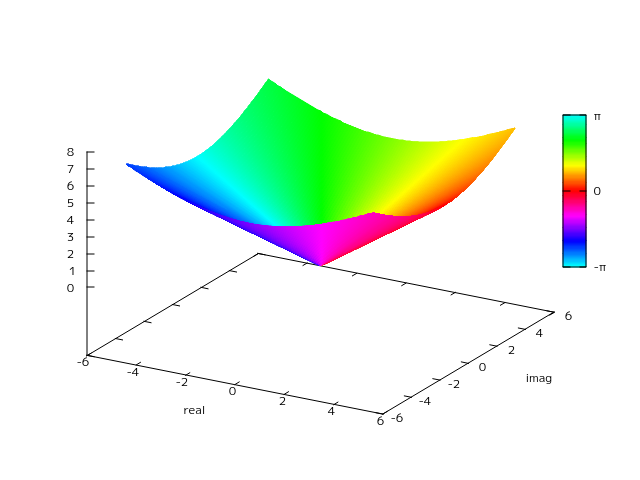
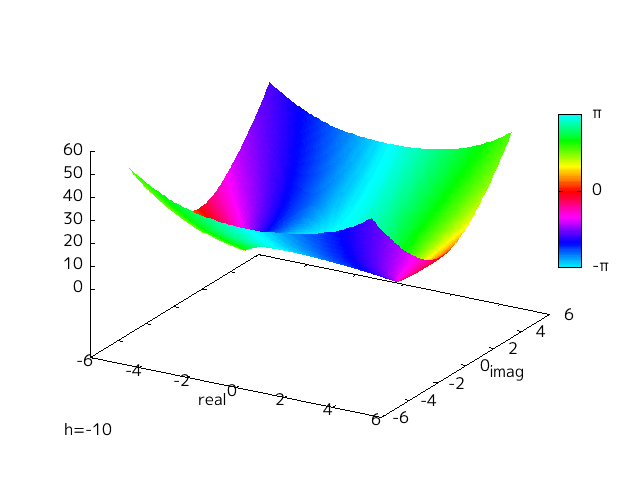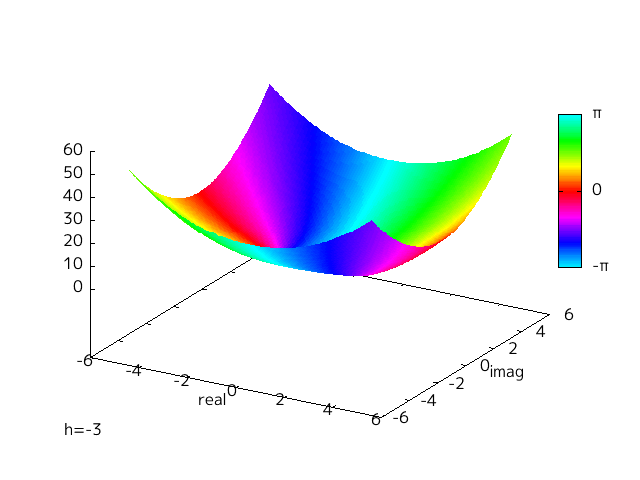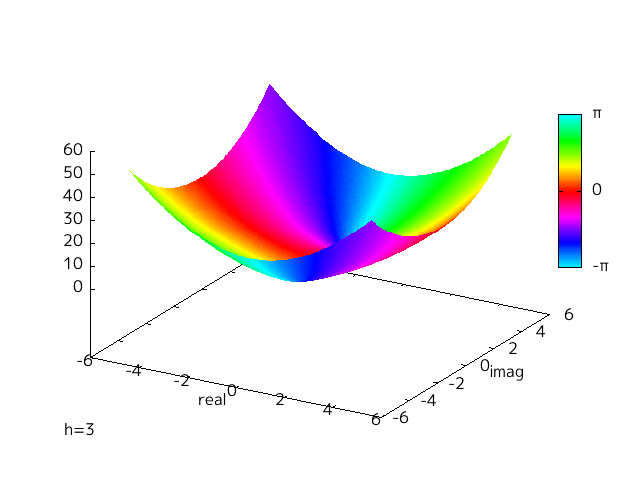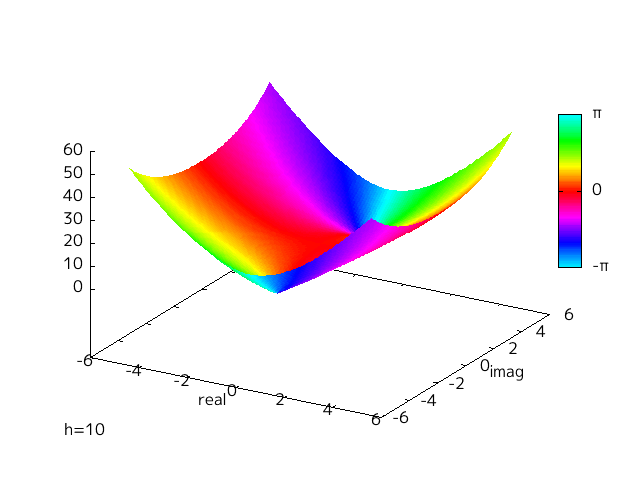
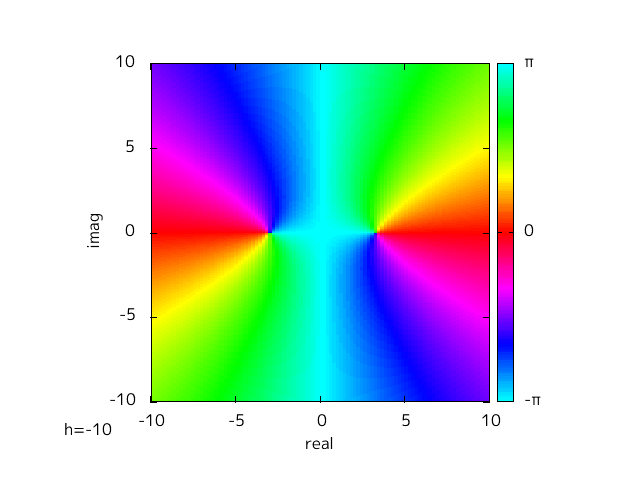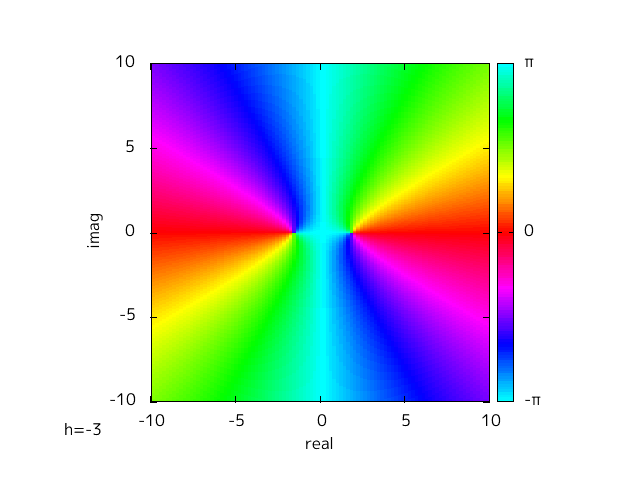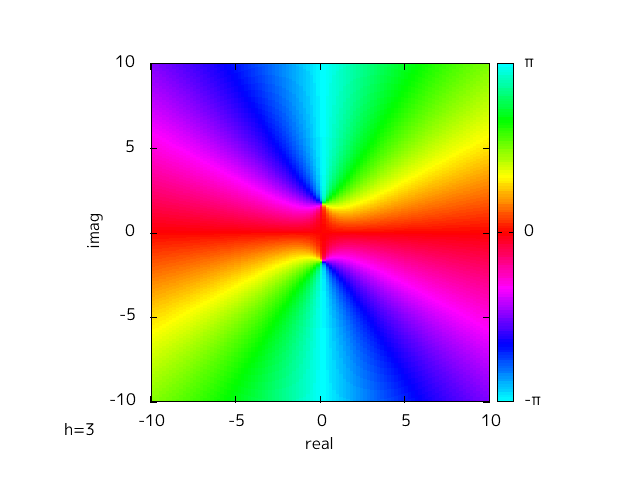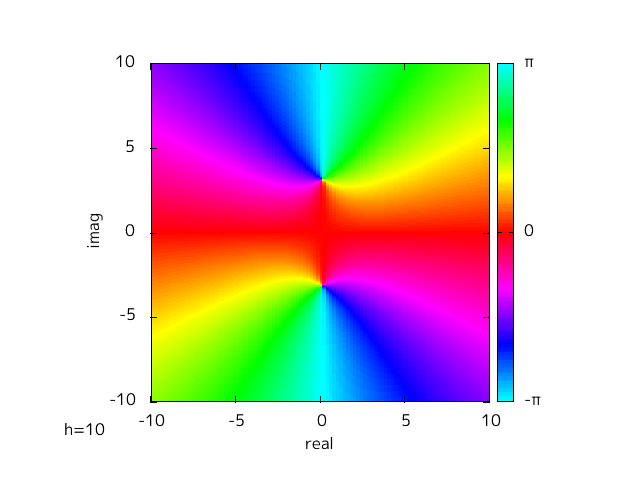
h を替えることによって変わってくるのだが、この変化を視覚的にみるために、 h を -10 から 10 に変えて Fig-1.1, 1.2 と同様にプロットした。
Fig-1.3 f(x)=x^2+h
Fig-1.4 argument of f(x)=x^2+h
上図を出力するための gnuplot のコード
#!/usr/bin/gnuplot
set cbrange [-pi:pi]
set cbtics ("-π" -pi, "0" 0, "π" pi)
set pm3d corners2color c1
set palette defined ( 0 0 1 1, 1 1 1 1 )
set isosamples 100, 100
set palette model HSV defined ( 0 0.5 1 1, 0.5 1 1 1, 0.5 0 1 1, 1 0.5 1 1 )
#set palette model HSV start 0.5 defined (0 0 1 1, 1 1 1 1)
set xlabel "real"
set ylabel "imag"
set nokey
I = {0,1}
f(x,h) = x**2 + h
set terminal gif animate delay 10
set output "double_root_color_anim_pm3d.gif"
set zrange [0:60]
do for [h=-10:10]{
set label 1 sprintf("h=%d", h) at screen 0.1,0.1 left
splot '++' using 1:2:(abs(f(x+I*y, h))):(arg(f(x+I*y, h))) with pm3d
#pause -1
}
set output
unset zrange
set isosamples 512, 512
set size square
set view map
set terminal gif animate delay 10
set output "double_root_color_anim_pm2d.gif"
do for [h=-10:10]{
set label 1 sprintf("h=%d", h) at screen 0.1,0.1 left
splot arg(f(x+I*y, h)) with pm3d
#pause -1
}
set output
hを変えていくことでゼロ点が実軸上と虚軸上を動いていく様子がわかる。
h = 0 を境目に実軸と虚軸が入れ替わったような対称的な様子がわかる。
このようにして domain coloring の色相が周回する場所という形で二次方程式の解の場所を確認することができた。
これで複素解析学の意味では「関数グラフの概形を見た」「虚数解を見た」と言える。
が、h を変える、すなわち関数値を実軸方向に増減させると、なぜこうなるのか?がいまいちわからない。
したがって、他の表示の仕方で概形を眺めたほうが良かろう。
実部と虚部でそれぞれ見る
実部
(1.3)の実部を計算する。
(1.3)に
x
=
a
+
b
i
x=a+bi
を代入すると
f
(
x
)
=
f
(
a
+
b
i
)
=
(
a
+
b
i
)
2
+
h
=
(
a
2
−
b
2
+
h
)
+
2
a
b
i
f(x)=f(a+bi)=(a+bi)^2+h=(a^2-b^2+h)+2abi
(1.4)
よって実部は
Re
f
(
a
+
b
i
)
=
a
2
−
b
2
+
h
\operatorname{Re} f(a+bi)=a^2-b^2+h
(1.5)
であり双曲放物面(hyperbolic paraboloid)となる。 h=0 のときの概形を下図に示す。
Fig-1.5 Re (x^2)
上図を出力するための gnuplot のコード
#!/usr/bin/gnuplot
set isosamples 50, 50
set xlabel "real"
set ylabel "imag"
unset key
I = {0,1}
f(x) = x**2
splot real(f(x+I*y)), \
[-10:10] "++" u ($1):(0):(f($1)) w l ls 2, \
[-10:10] "++" u (0):($1):(-f(-$1)) w l ls 3
pause -1
xが実軸上(b=0)のとき、自明ではあるが
f
(
a
)
=
a
2
+
h
f(a)=a^2+h
と下に凸となる放物線となる。
xが虚軸上(a=0)のとき、
f
(
b
i
)
=
−
b
2
+
h
f(bi)=-b^2+h
と上に凸となる放物線となる。
実軸上と虚軸上の場合の概形も上図に描き足した。
それぞれ緑色と水色で示した線である。
緑色の放物線を水色の放物線に沿って並行移動することでこの双曲放物面を形作ることができる。
また対称性に関して、
x
→
−
i
x
x \to - i x
と置き換えると同じ値になることからわかるとおり、グラフの実部と虚部を入れ替えて上下反転(関数値を-1倍)すると同じ概形となる。
このとき前述の緑色と水色で示した放射線は外見上入れ替わるような感じになる。
Fig-1.6 symmetry of Re (x^2)
上図を出力するための gnuplot のコード
#!/usr/bin/gnuplot
set isosamples 50, 50
set xlabel "real"
set ylabel "imag"
unset key
I = {0,1}
f(x) = x**2
splot real(f(x+I*y)), \
[-10:10] "++" u ($1):(0):(f($1)) w l ls 2, \
[-10:10] "++" u (0):($1):(-f(-$1)) w l ls 3
pause -1
虚部
(1.3)の虚部は(1.4)より、
Im
f
(
a
+
b
i
)
=
2
a
b
\operatorname{Im} f(a+bi)=2ab
(1.6)
この概形は下図のようになる。
Fig-1.6 Im (x^2)
上図を出力するための gnuplot のコード
#!/usr/bin/gnuplot
set isosamples 50, 50
set xlabel "real"
set ylabel "imag"
unset key
I = {0,1}
f(x) = x**2
splot imag(f(x+I*y)), "-" w l
0 -10 0
0 +10 0
-10 0 0
+10 0 0
e
pause -1
ここで(1.6)式には h が出てこず、 h がどんな値であっても一定である。
f
(
x
)
=
0
f(x)=0
のためには
Rm
f
(
x
)
=
0
\operatorname{Rm} f(x)=0
かつ
Im
f
(
x
)
=
0
\operatorname{Im} f(x)=0
であるから、この虚部(1.6)が 0 で、かつ実部の双曲放物面(1.5)が 0 になるものを探せば良い。
(1.6)が 0 となるのは、
a
=
0
a=0
または
b
=
0
b=0
すなわち実軸と虚軸になる。
なので(1.5)の実軸と虚軸において 0 になる点を探せば良い。
Fig-1.5 で示した緑色の放物線を水色の放物線が h によってどう変わるかを見れば良い。
解の位置
(1.5)の実軸と虚軸における双曲線、
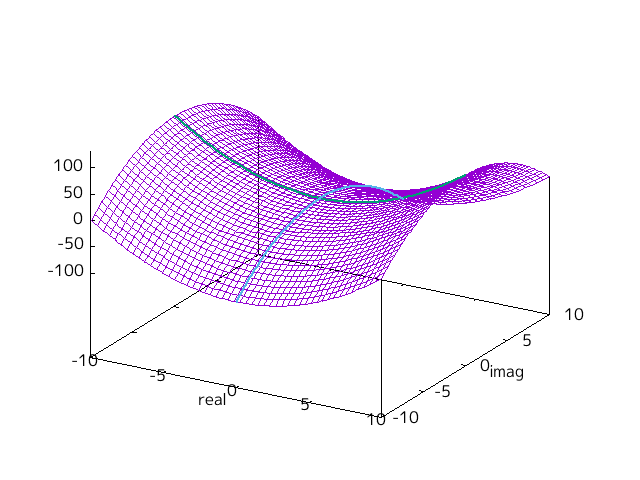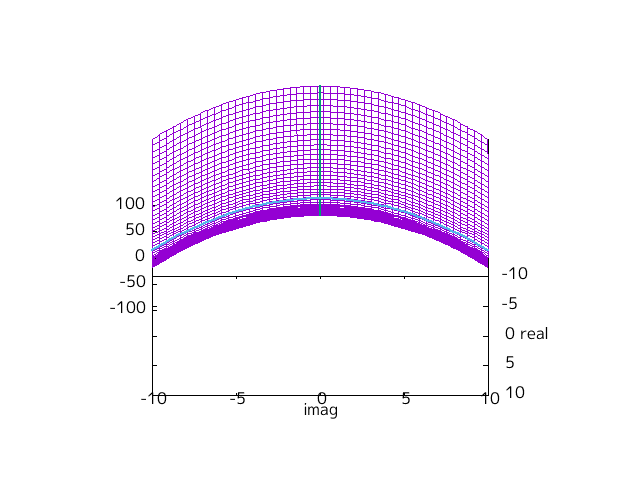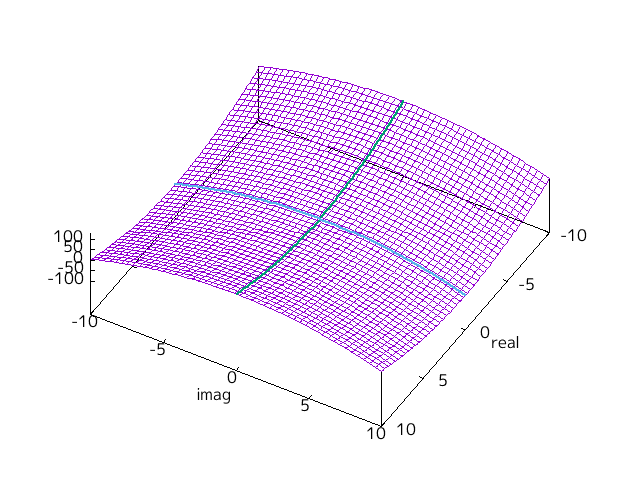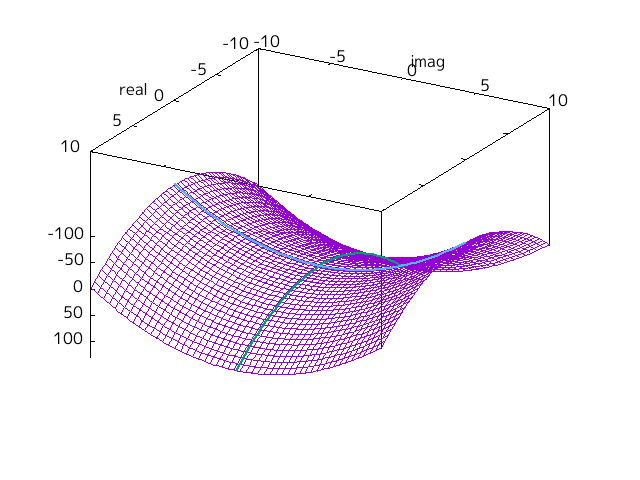
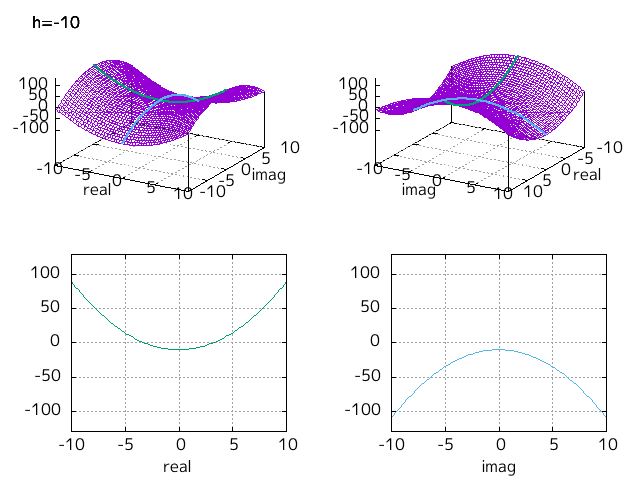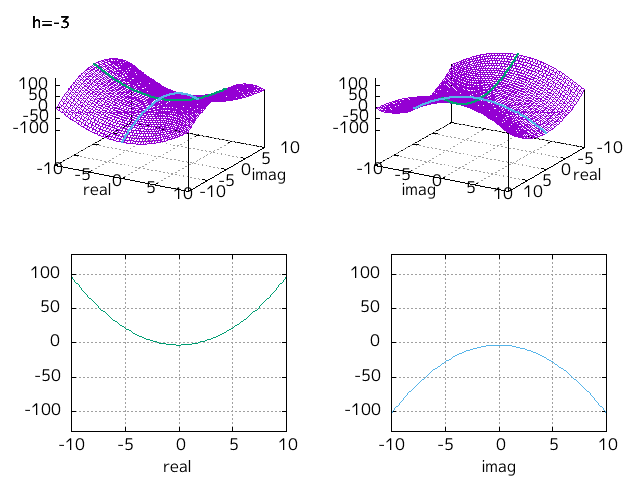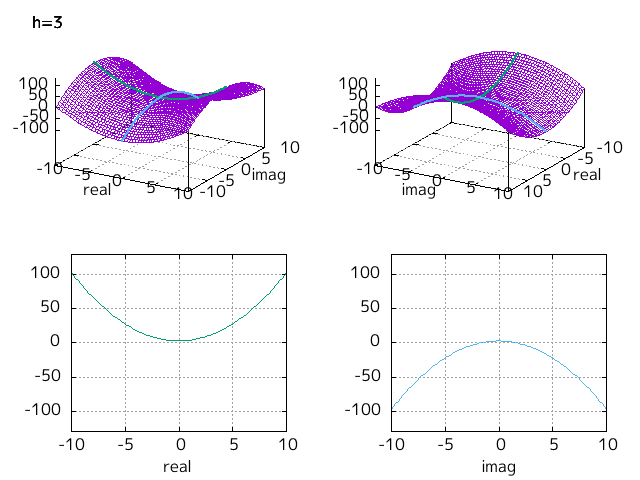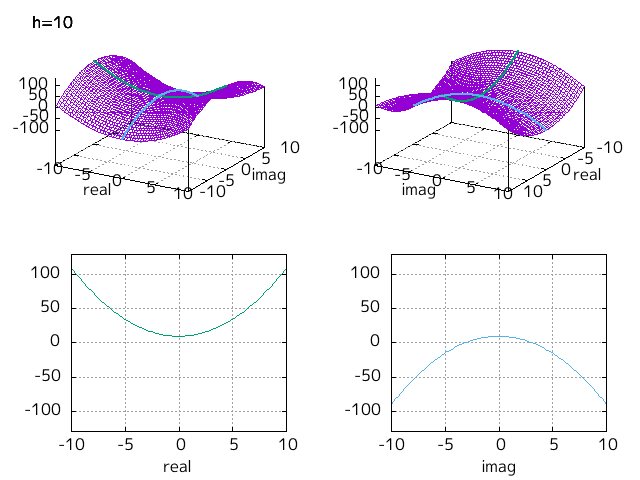
Fig-1.5 の緑色の放物線を水色の放物線が h を -10 から 10 まで変えるとどのように変わるかを示したのが下図となる。
Fig-1.7 x^2+h, h = -10,...,10
上図を出力するための gnuplot のコード
#!/usr/bin/gnuplot
set isosamples 50, 50
set nokey
I = {0,1}
f(x,h) = x**2 + h
set terminal gif animate delay 10
set output "double_root_shifting_anim.gif"
set grid
do for [h=-10:10]{
set multiplot layout 2,2
set xrange [-10:10]
set yrange [-10:10]
set zrange [-130:130]
set xlabel "real"
set ylabel "imag"
set label 1 sprintf("h=%d", h) at screen 0.05,0.95 left
set view 60, 30, 1, 1
splot real(f(x+I*y,h)), \
[-10:10] "++" u ($1):(0):(f($1,h)) w l ls 2 lw 2, \
[-10:10] "++" u (0):($1):(-f(-$1,-h)) w l ls 3 lw 2
set view 60, 30+90, 1, 1
replot
set xrange [-10:10]
set yrange [-130:130]
set xlabel "real"
set ylabel ""
plot real(f(x,h)) ls 2
set xlabel "imag"
set ylabel ""
plot real(-f(-x,-h)) ls 3
#pause -1
unset multiplot
}
set output
h < 0 では実軸上の放物線(緑色)が 0 となる点が 2 つあって、これが実数解である。
h > 0 では虚軸上の放物線(水色)が 0 となる点が 2 つあって、これが虚数解である。
h = 0 では両者の共通となるところとして重解となっている。
domain coloring での図示とちがって、 h を上下に動かすことによって解がどのように決まるかを視覚的に示すことができた。
虚数解を視覚的に存在することを図で確認することができた。
参考文献