ポニーテールの揺れの定式化と考察 (1/3)

このPostを読むにはMathMLをレンダリングできるFirefoxといったブラウザが必要です。もし数式部分が読めない場合は、 Firefoxをインストールするか MathMLの記述を画像に変換するなどをしてください。

ポニーテールを観察していると、その人がわざと揺らしているのではないかと思うほど、リズミカルに揺れています。その反面、あまり揺れていない人もいることに気づきました。どんな時によく揺れて、どんな風になるとあまり揺れないのでしょうか。そんな秘密を調べたい。

シゼコン　自然科学観察コンクールの 2008年度の一等賞の研究「 -ポニーテールはなぜ揺れる？- 振り子のふれ方の研究」はテーマの選定もさることながら、内容も興味深い。内容としては、ポニーテールを振り子にモデル化したうえで、実際にポニーテール共振器と振れ幅測定ボードを作り、実験考察をしている。

この研究の成果でもっとも重要なことは、以下の考察の部分であり、歩行のテンポと振り子リズムの共振の関係に言及していることだと思う。

振り子と体の動きをよく観察すると、振り子リズムのポイントは「足のウラ」でした。右足が地面に着く時、わずかに右肩が下がり、振り子も右側に最大にふれます。反対に左足が着地した時は、自然と左肩が下がり、振り子も左側に最大にふれます。歩くという運動は、このような動きのくり返しです。

というわけで、歩行のテンポと振り子リズムの関係について数式であらわせられないのか？数式化して、ポニーテールが揺れるための条件を明らかにしたい。

まず簡単のため、また筆者の復習のため、単振り子の挙動を考察する。単純に質量mのおもりが長さlの理想的な紐につながっている振り子を想定する。鉛直方向と紐がなす角がθであり、この角度の振る舞いをしらべる。

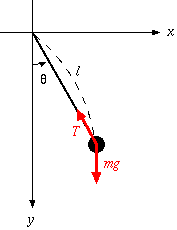
振り子のおもりに注目すると、運動方程式は、

m \frac{d^{2}}{d t^{2}} (\begin{matrix} x \\ y \end{matrix}) = m (\begin{matrix} 0 \\ - g \end{matrix}) - T (\begin{matrix} - \sin θ \\ - \cos θ \end{matrix})

(1.1)

また、振り子のひもの長さをlとして、

(\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} l \sin θ \\ l \cos θ \end{matrix})

(1.2)

さて、この単振り子の振れ幅は十分に小さいと仮定すると、 $\sin θ = θ$ であるので、(1.2)式は以下のように変形できる。

(\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} l θ \\ l \end{matrix})

(1.3)

(1.3)式を(1.1)式に代入することにより

(\begin{matrix} m l \frac{d^{2} θ}{d t^{2}} \\ 0 \end{matrix}) = (\begin{matrix} - T θ \\ m g - T \end{matrix})

(1.4)

鉛直成分から $T = m g$ であるので、水平成分から

m l \frac{d^{2} θ}{d t^{2}} = - m g θ

(1.5)

(1.5)式を整理すると、いわゆる振動方程式と呼ばれる二階微分方程式が得られる。

\frac{d^{2} θ}{d t^{2}} = - \frac{g}{l} θ

(1.6)

(1.6)式の特殊解は $θ = e^{\pm i \sqrt{g / l} t}$ であるので、(1.6)式の一般解は任意定数C₁,C₂を用いて以下のようになる。

θ = C_{1} e^{i \sqrt{g / l} t} + C_{2} e^{- i \sqrt{g / l} t}

(1.7)

ここで、(1.7)式に $C_{1} = \frac{A}{2} e^{i φ}, C_{2} = \frac{A}{2} e^{- i φ}$ を代入することにより、

θ = \frac{A}{2} (e^{i (\sqrt{g / l} t + φ)} + e^{- i (\sqrt{g / l} t + φ)})

(1.8)

したがって、よく知られた周期が $2 π \sqrt{l / g}$ である単振動の式(1.9)が得られる。

θ = A \cos (\sqrt{\frac{g}{l}} t + φ)

(1.9)

ただ、この単振り子は当然ながら、ポニーテールの振動を表現していない。次に、ポニーテール共振器の挙動について考察しよう。

ポニーテール共振器自体は単純な振り子なので単振り子と見なせる。その振り子の支点が強制振動として動いているとみなす。

なお強制振動は以下の式とする。

X (t) = X \cos ω t

(2.0)

微積分学観点から取り扱いやすいcosをつかったのであり、人の振動と正弦波形との関係はここでは考察しない。また、Xが紛らわしいとかあるがキニシナイ。

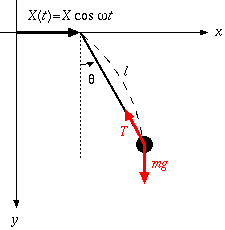
振り子のおもりに注目すると、運動方程式は、(1.1)式と完全に一致となるが、

m \frac{d^{2}}{d t^{2}} (\begin{matrix} x \\ y \end{matrix}) = m (\begin{matrix} 0 \\ - g \end{matrix}) - T (\begin{matrix} - \sin θ \\ - \cos θ \end{matrix})

(2.1)

また、振り子のひもの長さをlとして、

(\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} l \sin θ + X (t) \\ l \cos θ \end{matrix})

(2.2)

さて、この単振り子の振れ幅は十分に小さいと仮定すると、 $\sin θ = θ$ であるので、(2.2)式は以下のように変形できる。

(\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} l θ + X (t) \\ l \end{matrix})

(2.3)

(2.3)式を(2.1)式に代入することにより

(\begin{matrix} m l \frac{d^{2} θ}{d t^{2}} + m \frac{d^{2} X (t)}{d t^{2}} \\ 0 \end{matrix}) = (\begin{matrix} - T θ \\ m g - T \end{matrix})

(2.4)

鉛直成分から $T = m g$ であるので、水平成分から

m l \frac{d^{2} θ}{d t^{2}} = - m g θ - m \frac{d^{2} X (t)}{d t^{2}}

(2.5)

(2.5)式を整理して、振り子の関係を示した微分方程式が以下の式(2.6)である。

\frac{d^{2} θ}{d t^{2}} = - \frac{g}{l} θ - \frac{1}{l} \frac{d^{2} X (t)}{d t^{2}}

(2.6)

微分方程式を解くのは次回で。