ポニーテールの揺れの定式化と考察 (2/3)

このPostを読むにはMathMLをレンダリングできるFirefoxといったブラウザが必要です。もし数式部分が読めない場合は、 Firefoxをインストールするか MathMLの記述を画像に変換するなどをしてください。

前回から引き続き、ポニーテール共振器の運動について考察していこう。

3. ポニーテール共振器の挙動

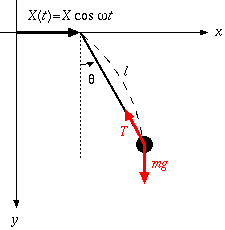
前回、ポニーテール共振器の運動方程式を解いて微分方程式を得た。式(2.6)であったが、再掲する。

\frac{d^{2} θ}{d t^{2}} = - \frac{g}{l} θ - \frac{1}{l} \frac{d^{2} X (t)}{d t^{2}}

(2.6)

(2.6)式について、強制振動の部分を展開する。（なお、前回の(2.0)式で強制振動の式を定義済み）すなわち、

\frac{d^{2} X (t)}{d t^{2}} = X \frac{d^{2}}{d t^{2}} \cos ω t = - X ω^{2} \cos ω t

(3.1)

を式(2.6)に代入する。

\frac{d^{2} θ}{d t^{2}} = - \frac{g}{l} θ - \frac{X ω^{2}}{l} \cos ω t

(3.2)

さて、この式(3.2)の二階微分方程式を解けばいい訳だが、結構複雑で面倒なので計算機で算出させた。つまり Mathematica といったものに例えば以下のようにコマンドを打てばよい。

In[*]:= DSolve[x''[t]==-g/l x[t] + X omega^2/l cos[omega t], x[t], t]

もっとも、最近では Wolfram|Alpha に式(3.2)を解かせることもできる。

手段はともかくとして、式(3.2)の解は下記の式(3.3)のようになる。

θ = C_{1} \cos \sqrt{\frac{g}{l}} t + C_{2} \sin \sqrt{\frac{g}{l}} t + \frac{X ω^{2} \cos ω t}{g - l ω^{2}}

(3.3)

この振り子であるが、最初は静止していて歩いたりすると振れるということであった。初期状態(t=0)では静止していて、そこから振り子の支点の強制振動による共振によって振り子が振れてくる。静止している状態では、重力の影響によって、振り子は真下に向くのであることも考え、初期状態のθについて、以下の条件が成立する。

[θ]_{t = 0} = 0, [\frac{d θ}{d t}]_{t = 0} = 0

(3.4)

(3.3)式に(3.4)式を代入すると、C₁,C₂は以下のように求まる。

C_{1} = \frac{- X ω^{2}}{g - l ω^{2}}, C_{2} = 0

(3.5)

(3.3)式に(3.5)式を代入して、ポニーテール共振器の振り子の振動式が求まった。

θ = \frac{X ω^{2}}{g - l ω^{2}} (\cos ω t - \cos \sqrt{\frac{g}{l}} t)

(3.6)

式(3.6)の括弧で囲まれた部分は振動を表していて、その前は振幅を表している。括弧で囲まれた部分に三角関数の和積の公式を適用させると、すっきりとした式になる。

θ = \frac{2 X ω^{2}}{g - l ω^{2}} \sin \frac{\sqrt{g / l} + ω}{2} t \sin \frac{\sqrt{g / l} - ω}{2} t

(3.7)

この(3.7)式をみると、振り子の支点の強制振動振幅Xに比例する。これは激しく体が揺れれば、ポニーテール（振り子）がより揺れる感覚は一致する。ただ、単なる比例係数であって、それ以上の効果はない。

一方強制振動の各周波数ωが与える影響はもっと複雑だ。振動項をみると $ω \to \sqrt{g / l}$ とすれば、振動項がゼロとなるので振動しなくなるように思える。しかし、振幅部分は無限大に発散するので、いわゆる∞×0の不定形となるので、単純に議論できない。

\begin{matrix} \frac{2 X ω^{2}}{g - l ω^{2}} & \to & \frac{2 X g / l}{g - l g / l} = \frac{2 X g / l}{g - g} \to \infty \\ \sin \frac{\sqrt{g / l} - ω}{2} t & \to & \sin \frac{\sqrt{g / l} - \sqrt{g / l}}{2} t = 0 \end{matrix}

(3.8)

この近傍は極限で求めなければならず、(3.7)式を $\lim_{a \to 0} \frac{\sin a}{a} = 1$ の式を使える形に変形した上で極限を取らなければならないのである。

θ = \cdot\cdot\cdot = \frac{2 X ω^{2} t}{l (\sqrt{g / l} + ω) (\sqrt{g / l} - ω) t} \sin \frac{\sqrt{g / l} + ω}{2} t \sin \frac{\sqrt{g / l} - ω}{2} t

(3.9)

ここで $\frac{\sqrt{g / l} - ω}{2} t$ は0に漸近するので、例の $\lim_{a \to 0} \frac{\sin a}{a} = 1$ の公式が使えて、

\lim_{ω \to \sqrt{g / l}} θ = \lim_{ω \to \sqrt{g / l}} \frac{X ω^{2} t}{l (\sqrt{g / l} + ω)} \sin \frac{\sqrt{g / l} + ω}{2} t = \frac{X \sqrt{g / l}}{2 l} t \sin \sqrt{\frac{g}{l}} t

(3.10)

を得る。時間に比例してに振幅が再現なく増幅・発散する式となった。ただ、θが十分小さい場合のみでしか運動方程式を解いていないので、厳密に言えば、この式が使えない領域まで振幅が大きくなる、というのが正しい。

以上より、ポニーテール共振器の挙動について（特異な状態をあらわした(3.10)式も含めて）数式で表すことができた。

次回はこの式を元に考察する。