ベジェ曲線の円の近似で90度以外でもよいが180度以上はよくない

ベジェ曲線の円弧についていままで90度で計算してきた。しかし、この数字に意味付けはなかった。ただ単にドローソフトがそういう実装になっていたからだ。

そこで、任意の中心角の円弧をベジェ曲線で曲線近似するときの制御点の位置を算出してみよう。

135degree arc using Bézier

AOBのなす角度を90度からθに拡張する。頂点Bはそのままで、 BB'が頂点Bでの接線、BB'の長さがκとする。 AA'が頂点Aでの接線、AA'の長さも対称性よりκである。

すると、各点の座標は下記のようになる

\begin{aligned} \text{A:}&(\cos\theta,\sin\theta)\\ \text{B:}&(1,0)\\ \text{A':}&(\cos\theta+\kappa\sin\theta,\sin\theta-\kappa\cos\theta)\\ \text{B':}&(1,\kappa)\\ \text{C:}&(\cos\frac{\theta}{2},\sin\frac{\theta}{2})\\ \end{aligned}

(3.1)

ベジェ曲線の定義より、ベジェ曲線上の任意の点はパラメータ $u(0\leq u \leq 1)$ を使って、下記の通りとなる：

\bm{P}(u)=\bm{A}(1-u)^3+\bm{A}'3u(1-u)^2+\bm{B}'3u^2(1-u)+\bm{B}u^3

(3.2)

ベジェ曲線の中間点Cはu=1/2として

\bm{P}\left(\frac{1}{2}\right)=\frac{\bm{A}}{8}+\frac{3\bm{A}'}{8}+\frac{3\bm{B}'}{8}+\frac{\bm{B}}{8}

(3.3)

となる。

(3.3)式に(3.1)の頂点データを代入することで、x座標成分として

\frac{1}{8}(4\cos\theta + 3\kappa\sin\theta + 4)

(3.4)

同様に、y座標成分として

\frac{1}{8}(4 \sin\theta + 3\kappa (1-\cos\theta))

(3.5)

が得られる。ここが円弧の中心点Cになるようにすればよい。

よって(3.4)式から

\begin{aligned} \cos\frac{\theta}{2}&=&\frac{1}{8} (4 \cos\theta + 3 \kappa \sin\theta + 4)\\ 8\cos\frac{\theta}{2}&=&4 \left(2\cos^2\frac{\theta}{2}-1\right)+6 \kappa \cos\frac\theta2 \sin\frac\theta2+4\\ 8\cos\frac{\theta}{2}&=&8 \cos^2\frac\theta2+6 \kappa \cos\frac\theta2 \sin\frac\theta2\\ \kappa&=&\frac{8 \cos\frac\theta2-8 \cos^2\frac\theta2}{6 \cos\frac\theta2 \sin\frac\theta2}\\ &=&\frac{4}{3} \left({\frac{1-\cos\frac\theta2}{\sin\frac\theta2}}\right)\\ &=&\frac{4}{3}\cdot\tan\frac\theta4 \end{aligned}

(3.6)

とκの値が得られた。

なお、この算出過程で $\theta = \pi \,\text{[rad]}\,(= 180\degree)$ を除外してしまっている。この場合のみだけ、y軸成分の(3.5)式から計算して出すと

\begin{aligned} \sin\frac\theta2&=&\frac{1}{8} (4 \sin\theta+3 \kappa (1-\cos\theta))\\ 0&=&\frac{1}{8} (0+3 \kappa (1-0))\\ \kappa&=&\frac{4}{3} \end{aligned}

(3.6)

となり、結局以下の単一の式で表現できる：

\kappa=\frac{4}{3}\cdot\tan\frac\theta4

(3.7)

アタリマエのことながら、この結果に対して $\theta = \pi/2 \,\text{[rad]}\,(= 90\degree)$ を代入することでよく知られた90度の場合のκの値が得られる。

\frac{4}{3}\cdot \tan\frac{\pi/2}{4}=\frac{4 (\sqrt{2}-1)}{3}

(3.8)

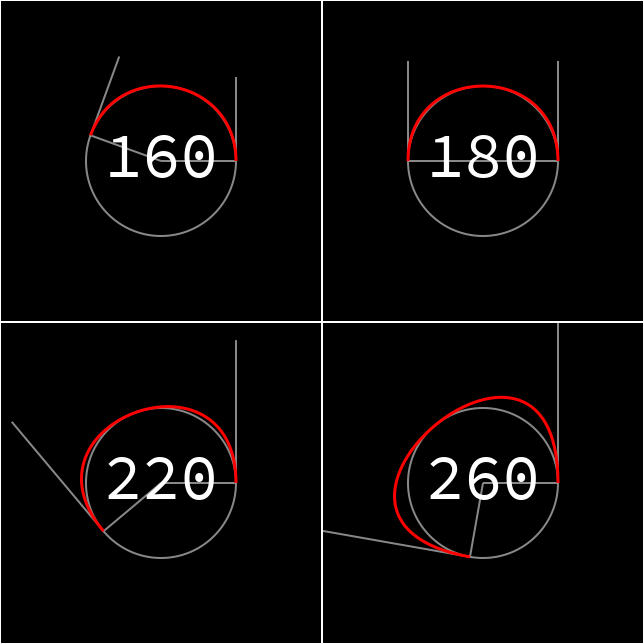
θを変えて描画させてみると、 180度まではまずまずの近似であるが、180度を超えるとかけ離れた概形になってしまう。 180度以上の円弧を描くときは分割が必須である。