ベジェ曲線で描く円弧と本物の円弧の差（中心角について一般化）

ベジェ曲線による円の描画の制御点の位置はなぜ0.55228…なのか?から始まり ベジェ曲線で描く円の誤差について ベジェ曲線で描く円と真円の差について にて議論した。 次に、ドローソフトで一般的な中心角90度に注目し、これを一般化したのが ベジェ曲線の円の近似で90度以外でもよいが180度以上はよくない ということであった。

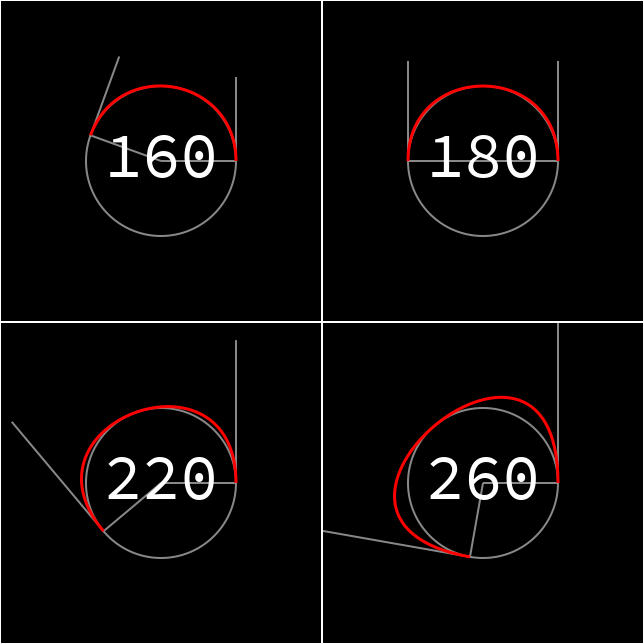
しかしベジェ曲線の円の近似で90度以外でもよいが180度以上はよくないでは、 中心角の大きさとベジェ曲線で描く円と真円の誤差の関係について定式化をしていなかった。 これは数式の途中式が複雑だったら投げ出していたのだが、 改めてmaxima使って解いてみるとシンプルにまとまった。

制御点の位置

前回とかぶるがまずは制御点の位置、要するにκを求める。

$$\bm{P}(u)=\bm{A}(1-u)^3+\bm{A}'3u(1-u)^2+\bm{B}'3u^2(1-u)+\bm{B}u^3$$

(4.1)

$$\begin{aligned} \text{A:}&(\cos\theta,\sin\theta)\\ \text{B:}&(1,0)\\ \text{A':}&(\cos\theta+\kappa\sin\theta,\sin\theta-\kappa\cos\theta)\\ \text{B':}&(1,\kappa)\\ \end{aligned}$$

(4.2)

このベジェ曲線の定義(4.1)式に、座標(4.2)を代入して x座標成分Px(u)とPy(u)を求める。

(%i1) P(u):=A*(1-u)^3+Ac*3*u*(1-u)^2+Bc*3*u^2*(1-u)+B*u^3;
                          3                 2         2              3
(%o1)    P(u) := A (1 - u)  + Ac 3 u (1 - u)  + Bc 3 u  (1 - u) + B u
(%i2) Px(u):=sublis([A = cos(theta),B = 1,Ac = cos(theta)+k*sin(theta),Bc = 1],P(u));
(%o2) Px(u) := sublis([A = cos(theta), B = 1, Ac = cos(theta) + k sin(theta), 
                                                                 Bc = 1], P(u))
(%i3) Py(u):=sublis([A = sin(theta),B = 0,Ac = sin(theta)-k*cos(theta),Bc = k],P(u));
(%o3) Py(u) := sublis([A = sin(theta), B = 0, Ac = sin(theta) - k cos(theta), 
                                                                 Bc = k], P(u))

ベジェ曲線の中間点u=1/2に注目してκの値を得る。

(%i4) solve([Px(1/2) = cos(theta/2)],k);
                                                theta
                           4 cos(theta) - 8 cos(-----) + 4
                                                  2
(%o4)               [k = - -------------------------------]
                                    3 sin(theta)

ここからmaximaは簡略化がたいして出来ないのであるが、 theta/4を使うことを明示的に指示すれば簡略化ができることに気づいた。 つまりtheta/4を明示的に他の変数tに書き換えた上で簡略化を指示した。

(%i5) sublis([theta = 4*t],%);
                             4 cos(4 t) - 8 cos(2 t) + 4
(%o5)                 [k = - ---------------------------]
                                     3 sin(4 t)
(%i6) trigsimp(%),trigexpand;
                                     4 sin(t)
(%o6)                           [k = --------]
                                     3 cos(t)

これより、κの値が求まった。

$$\kappa=\frac{4}{3}\cdot\tan\frac\theta4$$

(4.3)

ベジェ曲線で描く円と真円の差、一般化。

ベジェ曲線で描く円と真円の差についてと同じように解く、力技で。

ベジェ曲線の近似円弧の半径方向の大きさPp(u)は：

(%i7) Pp(u):=Px(u)^2+Py(u)^2;
                                      2        2
(%o7)                      Pp(u) := Px (u) + Py (u)

これをθ=90度で計算したときと同様に微分=0の式を立てる。

(%i8) diff(sublis([k = 4/3*tan(theta/4)],Pp(u)),u) = 0$
(%i9) sublis([theta = 4*t],%);
              4 tan(t) sin(4 t)
(%o9) 2 (- 6 (----------------- + cos(4 t)) (1 - u) u + 6 (1 - u) u
                      3
      4 tan(t) sin(4 t)                    2                     2
 + 3 (----------------- + cos(4 t)) (1 - u)  - 3 cos(4 t) (1 - u) )
              3
   3              2      4 tan(t) sin(4 t)                    2
 (u  + 3 (1 - u) u  + 3 (----------------- + cos(4 t)) (1 - u)  u
                                 3
                   3                   2
 + cos(4 t) (1 - u) ) + 2 (- 4 tan(t) u
                 4 tan(t) cos(4 t)
 - 6 (sin(4 t) - -----------------) (1 - u) u + 8 tan(t) (1 - u) u
                         3
                 4 tan(t) cos(4 t)         2                     2
 + 3 (sin(4 t) - -----------------) (1 - u)  - 3 sin(4 t) (1 - u) )
                         3
                    2                 4 tan(t) cos(4 t)         2
 (4 tan(t) (1 - u) u  + 3 (sin(4 t) - -----------------) (1 - u)  u
                                              3
                   3
 + sin(4 t) (1 - u) ) = 0
(%i10) trigsimp(trigexpand(%));
                 6     5          6     4          6     3          6     2
(%o10) - (384 sin (t) u  - 960 sin (t) u  + 832 sin (t) u  - 288 sin (t) u
                                                      6           2
                                              + 32 sin (t) u)/(sin (t) - 1) = 0

なお、(%o8)はあまりにも長いので出力を省略した。 ともあれこちらについても theta/4を明示的に他の変数tに書き換えた上で簡略化を指示することで かなり式が簡単になっていると思う。

これを解くと

(%i11) solve(%,u);
                       1        sqrt(3) - 3      sqrt(3) + 3
(%o11)     [u = 1, u = -, u = - -----------, u = -----------, u = 0]
                       2             6                6

この解のうち、u=0,1/2,0 は、ベジェ曲線の位置と円が一致するところでありPp(u)が極小（最小）値となるのである。 極大値をとるuは以下の２つである。

$$u=\frac{3\pm \sqrt{3}\,}{6}=\frac{1}{2}\pm\frac{\sqrt{3}\,}{6}$$

(4.4)

これはベジェ曲線で描く円と真円の差についての(2.7)式と完全に同一であり、 ベジェ曲線で描く円と真円の差が最大となる位置に中心角θが依存していない ことがいま示された。

そして最大値を求めるには、このときのPp(u)の値であるからにして：

(%i12) sublis([k = 4/3*tan(theta/4),u = (sqrt(3)+3)/6],Pp(u))$
(%i13) trigsimp(trigexpand(sublis([theta = 4*t],%))),factor;
                            2               2        2
                        (sin (t) + 3) (2 sin (t) - 3)
(%o13)                  ------------------------------
                                        2
                                  27 cos (t)

すなわち最大値は：

$$\left\|\bm{P}\left(\frac{1}{2}\pm\frac{\sqrt{3}}{6}\right)\right\|=\sqrt{\frac{\left(\sin ^2\frac{\theta}{4}+3\right)\left(2\sin ^2\frac{\theta}{4}-3\right)^2}{{27 \cos ^2\frac{\theta}{4}}}\,}$$

(4.5)

なお、中心角90度について求めると、 ベジェ曲線で描く円と真円の差についての(2.8)式と同一の結果が得られるので 確かに一般化した式であるとわかる。

(%i14) limit((%o13), t, %pi/2/4)$
(%i15) float(sqrt(%));
(%o15)                         1.000272530007428

さて、(4.5)式をグラフ化する。

(%i16) deg_to_rad(d) := %pi * d / 180$
(%i17) plot2d(sublis([theta=deg_to_rad(theta)], limit(sqrt(%o13), t, theta/4)),
       [theta, 0, 270], [ylabel, "Pmax"])$

なおここで、0〜270度しかプロットしていないのは、360度までプロットすると無限大に発散してしまうからである。

(%i18) limit((%o13), t, 2*%pi/4);
(%o18)                                    inf

単調増加で中心角が増えると急激に1から離れていく様子がわかる。 前回 ベジェ曲線の円の近似で90度以外でもよいが180度以上はよくない といったが、これは撤回、 実際にどこまで誤差を認めるかをベースに考えるのが良さそうだ。