ポニーテールの揺れの定式化と考察 (3/3)

このPostを読むにはMathMLをレンダリングできるFirefoxといったブラウザが必要です。もし数式部分が読めない場合は、 Firefoxをインストールするか MathMLの記述を画像に変換するなどをしてください。

4. ポニーテール（振り子）の振れ方の考察

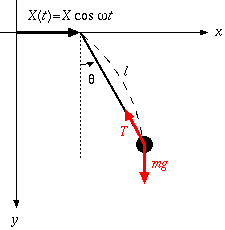
前回まででポニーテール共振器の挙動を定式化することができた。その成果である(3.7)式を再掲する。なお、 $ω \to \sqrt{g / l}$ 近傍では時間に比例して振幅が増幅され、やがてθが微小という前提条件から外れてしまう。

θ = \frac{2 X ω^{2}}{g - l ω^{2}} \sin \frac{\sqrt{g / l} + ω}{2} t \sin \frac{\sqrt{g / l} - ω}{2} t

(3.7)

(3.7)式で表される振り子共鳴器の振動の振幅である

Θ = \frac{2 X ω^{2}}{g - l ω^{2}}

(4.1)

に注目したい。この支点の振動振幅Xは単なる比例定数としてしか作用しないのでここには特に注目する必要はない。（いっぱい揺らせば、それだけ揺れるだけということ。）

(4.1)式のωに注目して傾向をみると、

ω=0のとき、Θ=0
$0 \leq ω \leq \sqrt{g / l}$ のとき、Θは単調増加
$ω = \sqrt{g / l}$ のとき、Θは正の無限方向に発散（もっとも(3.7)式自体が発散するので(4.1)式は適用できないが、前回検討したように振幅自体は発散しているので、これで良しとしよう。）
$ω \geq \sqrt{g / l}$ のとき、Θは負の無限から、単調増加して、
$ω \to \infty$ のとき、Θは $- 2 X / l$ に漸近する

のであるが、実際は増減がかなり激しいグラフとなる。参考までに、l=0.15[m]のときの $| Θ / X |$ の関係を示す。なお縦軸は対数スケールであることに注意されたい。

さて、実際に「 -ポニーテールはなぜ揺れる？- 振り子のふれ方の研究」での実験1の結果と比較していく。以下「実験1の結果」といったように記載されているのは、すべてその文献に記載されている値である。

実験1の方法に記述されている実験パラメータは以下の通り。

糸の長さを変え（15㎝、30㎝、60㎝）、歩く速さを変えて（ゆっくり、普通、早足で）、６m歩いた時の振り子の往復回数をそれぞれ５回ずつ計る。おもりは50円玉１枚（＝４g）。

糸の長さはlに対応するのは明らかだが、歩く速度は強制振動に対応するであろう。考察に書かれているように足の着地が振動の端っこになるので、 10秒で10歩歩いた時は2秒周期の振動になる。

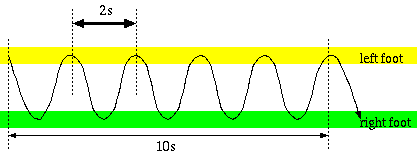
歩くテンポ（速度）とωの関係は以下のようになる。

テンポ	歩行間隔	周期	`ω`
ゆっくり歩いた	20歩で約20秒	2秒	`π`
普通に歩いた	20歩で約10秒	1秒	2`π`
早足で歩いた	20歩で約5秒	0.5秒	4`π`

(4.1)式に実験1のパラメータを入れて計算をする。表中の値はΘ/Xであり、単位は[rad/m]である。

振り子の長さ`l`	0.15m	0.30m	0.60m
ゆっくり歩いた（20歩で約20秒）	2.37	2.89	5.09
普通に歩いた（20歩で約10秒）	20.4	-38.6	-5.67
早足で歩いた（20歩で約5秒）	-22.7	-8.41	-3.72

支点の振動振幅幅Xで割っているので、数値の大小だけに注目してほしい。「ゆっくり歩いた」では60cmが最も揺れ、「普通に歩いた」や「早足で歩いた」では60cmは他と比べ揺れは小さい。

この表中の値はΘ/Xと絶対値を敢えて外して書いた。こうすることで、正負の間に相当するところで発散する（もっともポニーテールが揺れる）パラメータが存在することが容易にわかるためだ。例えば長さ l=0.15 m でいえば、20歩で7.8秒（周期0.78秒）程度のところが発散するパラメータであり「普通に歩いた」と「早足で歩いた」の間である。また、普通に歩いた（20歩で約10秒）（周期1秒）でいえば、l=0.25 m のところが発散するパラメータである。

この結果は、実験1の結果と「ゆっくり歩いた」と「普通に歩いた」では傾向とは一致した。しかし、「早足で歩いた」では実験では30cmが最も揺れるのに、この式での計算では15cmが最も揺れた。また、歩くスピードで比較しても実験結果と合わないが、こちらにかんしては振動振幅幅Xが、歩くスピードで変わってしまう（速く歩くと揺れやすい）からではないか。

5. 考察と感想

ポニーテールをモデル化したポニーテール共振器の挙動について定式化をした。その結果、ポニーテールの長さと体の動き（横振れ周期）の関係が重要な影響があることがわかった。このモデルでは、ポニーテールを振り子とみなしたときの固有周期とほぼ同じ周期で横揺れするような速度で歩いたときにポニーテールの振れ幅は大きくなる。

一方で実験結果と一致しない点、特に体の動きのモデル化は不十分であることがわかった。すなわち、早く歩いたときどのように体は揺れるかなどである。今回は理想的に一定の振幅の波形としたが、この場合に歩行速度で比べた振れ幅の比較ができなかった。今後、歩くときの振動についてよりよいモデル化が必要と思われる。

A. 参考文献

中村優里:「-ポニーテールはなぜ揺れる？- 振り子のふれ方の研究」シゼコン　自然科学観察コンクール　第49回、2008年。
三宅敏恒：『入門微分積分』培風館、1992年