メトロポリス（Metropolis）という英字フリーペーパー（オンラインでも見れる）に、日本のバレンタインデーのマーケティング戦略について、興味深い言及がなされているのを見つけた。

Japanese chocco companies' marketing technique can't be faulted, with every human relationship now requiring some kind of sugary gift on February 14.

和訳すると以下のような感じだろうか（もうちょっとマトモな和訳はできないものかのぅ）。

日本のチョコレート菓子メーカのマーケティングとして、 すべての人間関係について2/14になんらかの甘いお菓子の贈り物が必要ということにするのに失敗できない。

2000年ごろから、 愛する男の人にチョコレートを贈るだったものから、贈る相手が広がっり昔と異なる様相になって来ているようだ。 それをメトロポリス誌の記事では、人間関係（human relationship）に注目している。 様々な人間関係があるが、それら全てにsome kind of sugary giftを関連付けようとしている、と。 そのような点で「今年も女の子からチョコレートを貰えなかった」という台詞のは、もはやバレンタインデー市場のトレンドに即していないと言えるのではないか。

普通市場規模というと単価×人数で計算するが、バレンタインデーの場合は人数じゃなくて人間関係なのだ、となると非常に興味深い。

古典的なチョコレートのプレゼントとグラフ理論

古典的な日本のバレンタインデーは「愛する男の人にチョコレートを贈る」ものである。 男女それぞれ5人の閉じられたコミュニティがあるとき、古典的日本的バレンタインデーの市場規模は高々5人(×単価)である。

高々5人と高々という語を使ったのは、「愛する男の人がいない女の人」の存在や「バレンタインデーに参加する気がない女の人」の存在のためである。

古典的日本的バレンタインデーのモデル(Classical Japanese St. Valentine day Model; CJSVMと以下略す)でチョコレートの受け渡し関係を図にすると、シンプルな有向グラフ(digraph; directed graph)になることがわかる。 女の人の集合をF、男の人の集合をMと表すと、CJSVMの有向グラフは以下の特徴を持つ。

  1. 頂点(vertex)集合Vは、FとMの直和である。 V=F+M.
  2. 弧(arc)集合Aは、F×Mの部分集合である。 A⊆F×M.
  3. Fのおのおのの要素について、出次数(outdegree)は0または1である。
  4. Mのおのおのの要素について、入次数(indegree)は0であることもある。
#F=#M=5のCJSVMの例

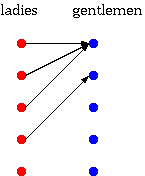
上の図では1人の男の人にチョコレートが集中し、3人がチョコレートが貰えないという図を描いた。 人間関係は次数分布がべき乗に従うスケールフリー性があると言われており、それに準じたためである。 ただ、弧の本数の引き方（誰がチョコレートをもらうか、もらえないか）については複雑ネットワーク（complex network）の理論が必要であるため、本稿で細かく議論する気はない。

CJSVMの枠組みで市場を広げるには、

  • 単価を増やす（チョコレートの高級化）
  • チョコレートを渡す文化の普及（参加人数の割合を増やす）

である。そしてこれは自ずと限界があるのが直感的にわかる。

義理チョコのグラフ理論

義理チョコ（Giri choco）というのは、本命チョコと対照的に説明される。 シンプルに言えば、「愛する人」でない男の人にもチョコレートを渡そうということである。

義理チョコを何も考えずに図に起こすと以下のような感じになる。

#F=#M=5のGCBMの例

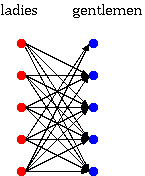
義理チョコはコミュニティー内の男の人にとにかく渡すので、義理チョコブロードキャストだ。 この義理チョコブロードキャストモデル（Giri-Choco Broadcasting Model; 以下GCBMと略す）は以下の特徴を持つ。

  1. 頂点集合Vは、FとMの直和である。 V=F+M.
  2. 弧集合Aは、F×MからCJSVMの弧集合(本命)を引いたものである。 A=F×M - ACJSVM.
  3. Fのおのおのの要素について、出次数は#Mまたは(#M-1)である。

ただ、義理チョコは単価が安いし、女の人の負担も大きい（Fのおのおのの要素について出次数が大きい）ため今日では減少傾向であるらしい。

友チョコのグラフ理論

CJSVMやGCBMの中では、あくまで渡す人を増やす、渡される人を増やすという人の数という古典的なマーケティング手法がとられる。 しかし、ある時からそれ異なるバレンタインデーのマーケティングが始まることになったと思う。 それが友チョコ（Tomo choco）だ。

友チョコというのは、主に女性たちの間で友人どうしで受け渡しするチョコレート。 ここで注目するのは人の数に注目したのではなく、人間関係に注目したことである。

#T=5のTCEMの例

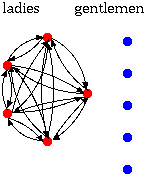
友チョコの交換のモデル（Tomo-Choco Exchange Model; 以下TCEMと略す）の特徴は以下の通り。

  1. 頂点集合Vは、友達クラスターの頂点集合Tに等しい。また、大抵の場合TはFの部分集合である。 V=T.
  2. 弧集合Aは、頂点集合V=Tの完全グラフの弧集合に等しい。。
  3. Tのおのおのの要素について、出次数・入次数ともに(#T-1)である。

これまでのCJSVMやGCBMのモデルと以下の点で根本的に異なっている。

  • チョコレートをプレゼントする頂点部分集合とプレゼントされる頂点部分集合の2つに分けることができなくなった。（CJSVMやGCBMでは出次数が0か、または入次数が0であった）
  • チョコレートを渡す人は受け取る人でもある。（弧について、始点と終点を逆にした弧もまた弧集合に含まれる）

弧集合の数は#A=#T(#T-1)であり、 友チョコ交換の参加人数(#T)が少なくても弧集合の数(#A)は大きい。 これは消費者の数が増えなくとも、人間関係（弧集合の数）に注目すれば市場が飛躍的に拡大する潜在性があるということを示唆しており非常に面白い。

補足：自分用チョコのグラフ理論

自分用にチョコレートを買った場合は、グラフ理論的に説明できないだろうと思いきや、説明できる。 自分へのご褒美（）というぐらいなので自己ループだ。

自分用チョコの例

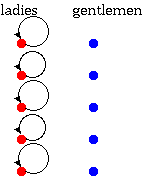
皮肉れた見方をすれば友チョコの自己完結版と言うべきかもしれない。 自分自身がチョコレートを渡す人でも受け取る人でもあるから。

Reference