前回の記事で、
|
|
(2.1) |
のとして、下記の頂点A,Bおよび制御点A',B'で中心角90度の円弧を
近似したベジェ曲線を描いていることを紹介した。
- A: (0, 1)
- B: (1, 0)
- A': (κ, 1)
- B': (1, κ)
90degree arc using Bézier
このとき、本物と円とどのような差があるのか考察したい。
ベジェ曲線の近似円弧の解析
ベジェ曲線の定義より、ベジェ曲線上の任意の点はパラメータを使って、下記の通り表現できる。
|
|
(2.2) |
(2.2)式に頂点座標を入れることで、ベジェ曲線による近似円弧のx座標、y座標が得られる:
|
|
(2.3) |
ベジェ曲線の近似円弧の半径方向の大きさは、
|
|
(2.4) |
u=0,1/2,1のときにこの値が1になることに注目して、
下式のように変形する。
|
|
(2.5) |
(2.5)式から、
u=0,1/2,1のときに最小値1を取る六次関数になることがわかる。
グラフの概形を描くと、下の図のようになる。
(六次関数らしさを出すためにあえてuの範囲外もプロットしてある)
(2.5)式の図示
さて、最大値について調べるために微分=0を計算する。
|
|
(2.6) |
この5つの解のうち、下の2つの解が最大値をとるuの値である。
|
|
(2.7) |
この結果と(2.5)式より最大値がわかる。
|
|
(2.8) |
また、このとき円弧上のどのあたりなのかを把握するために、
角度をもとめると
|
|
(2.9) |
数値を求めると以下の角度である:
もちろんこの2つは45度を軸に対称的な位置である。
ちなみに、
先程示したグラフの横軸を 0 →1 を 0 →90度と読みかえて
見てしまってもよい近似だったりする。
まとめ
ベジェ曲線の近似円弧における真円との差異について、下記特徴があることがわかった。
- ベジェ曲線の近似円弧の方が、真円よりも若干大きい
- 0度、45度、90度の部分は円と重なる
- 19.44度、70.56度あたりが円と差があるところであり、半径の0.00027倍程度の誤差がある
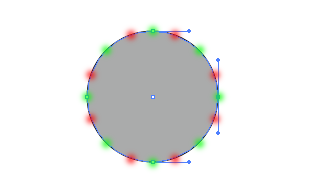 円と誤差の関係。緑付近は正確、赤付近は若干真円よりも大きい
円と誤差の関係。緑付近は正確、赤付近は若干真円よりも大きい
ベジェ曲線を使う限り円の精度は有効数字4桁程度といったところのようである。
補足:「時空の裂け目」
イラレの円は本当は円じゃない(もしくは時空の裂け目について)
にて45度回転させているが、
以上で述べた結論からいうと19.44度ぐらいのほうが
ふたつの円の差(時空の裂け目)が良く見える。
参考文献
